Assessing the Aerodynamics of an Able-Bodied Cyclist and Shoulder-Amputee Cyclist by Computer Fluid Dynamics
Evaluando la Aerodinámica de un Ciclista sin Discapacidad y un Ciclista con Amputación de Hombro Mediante Dinámica de Fluidos
Pedro Forte, Daniel A. Marinho, Henrique P. Neiva, Jorge E. Morais, Tatiana Sampaio, José E. Teixeira, Luís Branquinho, Antonio J. Silva, Antonio M. Monteiro, Tiago M. Barbosa
Assessing the Aerodynamics of an Able-Bodied Cyclist and Shoulder-Amputee Cyclist by Computer Fluid Dynamics
Cultura, Ciencia y Deporte, vol. 19, no. 62, 2024, https://doi.org/10.12800/ccd.v19i62.2188
Universidad Católica San Antonio de Murcia
Pedro Forte  *
*
Department of Sports, Higher Institute of Educational Sciences of the Douro, Portugal
Department of Sports, Instituto Politécnico de Bragança, Portugal
Research Center for Active Living and Wellbeing (Livewell), Instituto Politécnico de Bragança, Portugal
Research Center in Sports, Health and Human Development, Portugal
Research Center in Sports, Health and Human Development, Portugal
Department of Sports, University of Beira Interior, Portugal
Research Center in Sports, Health and Human Development, Portugal
Department of Sports, University of Beira Interior, Portugal
Department of Sports, Instituto Politécnico de Bragança, Portugal
Research Center for Active Living and Wellbeing (Livewell), Instituto Politécnico de Bragança, Portugal
Department of Sports, Instituto Politécnico de Bragança, Portugal
Research Center for Active Living and Wellbeing (Livewell), Instituto Politécnico de Bragança, Portugal
Research Center in Sports, Health and Human Development, Portugal
Department of Sports, Instituto Politécnico de Bragança, Portugal
Research Center for Active Living and Wellbeing (Livewell), Instituto Politécnico de Bragança, Portugal
Research Center in Sports, Health and Human Development, Portugal
Department of Sports, Polytechnic Institute of Guarda, Portugal
SPRINT—Sport Physical Activity and Health Research & Innovation Center, Guarda, Portugal
Research Center in Sports, Health and Human Development, Portugal
Biosciences Higher School of Elvas, Polytechnic Institute of Portalegre, Portugal
Life Quality Research Center (LQRC-CIEQV), Portugal
Research Center in Sports, Health and Human Development, Portugal
Department of Sports Sciences, University of Trás-os-Montes e Alto Douro, Portugal
Department of Sports, Instituto Politécnico de Bragança, Portugal
Research Center for Active Living and Wellbeing (Livewell), Instituto Politécnico de Bragança, Portugal
Department of Sports, Instituto Politécnico de Bragança, Portugal
Research Center for Active Living and Wellbeing (Livewell), Instituto Politécnico de Bragança, Portugal
Received: 20 march 2024
Accepted: 31 july 2024
Abstract: This study aimed to analyse the aerodynamics by numerical simulations with computer fluid dynamics of an able-bodied cyclist and a shoulder-amputee cyclist. An elite cyclist volunteered for this research; the cyclist was scanned with his competition gear and bicycle and the able-bodied and shoulder amputee 3D cyclists models were created. Numerical simulations were conducted between 1 m/s and 13 m/s (with increments of 1 m/s) with the fluent code. The effective surface area (ACd) varied between 0.38 and 0.59 m2 for the able-bodied cyclist; whereas, for the shoulder-amputee, it varied between 0.29 m2 and 0.62 m2. The ACd difference between the able-bodied and the amputee ranged from 3% to 28% and the drag differed between 2% and 19%. The drag coefficient ranged between 0.55 and 0.84 for the able-bodied and from 0.45 and 0.92 for the shoulder-amputee. The drag ranged across the different velocities (1-13 m/s) from 0.36 N – 39.25 N for the able-bodied cyclist and for the shoulder-amputee between 0.38 N – 31.69 N. The two cyclist models presented significant differences and small effect sizes (t = 2.720; p = 0.019; d = 0.18). The linear regression models computed the drag differences between the able-bodied and the disabled cyclist; a significant relationship and very high effect sizes for drag (R2 = 0.997; R2a = 0.995; SEE = 0.996; p < 0.001) were observed. This study allowed us to conclude that the shoulder-amputee cyclist presents a lower drag compared to the able-bodied one.
Keywords: Cycling, CFD, able-bodied, drag, paralympic.
Resumen: Este estudio tuvo como objetivo analizar la aerodinámica mediante simulaciones numéricas con dinámica de fluidos computacional de un ciclista sin discapacidad y un ciclista con amputación de hombro. Un ciclista de élite se ofreció como voluntario para esta investigación; el ciclista fue escaneado con su equipo de competición y bicicleta, y se crearon modelos tridimensionales de ciclistas con y sin discapacidad de hombro. Se realizaron simulaciones numéricas entre 1 m/s y 13 m/s (con incrementos de 1 m/s) con el código Fluent. El área efectiva de superficie (ACd) varió entre 0.38 y 0.59 m2 para el ciclista sin discapacidad, mientras que para el ciclista con amputación de hombro varió entre 0.29 m2 y 0.62 m2. La diferencia de ACd entre el ciclista sin discapacidad y el amputado de hombro osciló entre el 3% y el 28%, y la resistencia varió entre el 2% y el 19%. El coeficiente de resistencia varió entre 0.55 y 0.84 para el ciclista sin discapacidad y entre 0.45 y 0.92 para el ciclista con amputación de hombro. La resistencia varió en las diferentes velocidades (1-13 m/s) desde 0.36 N hasta 39.25 N para el ciclista sin discapacidad y desde 0.38 N hasta 31.69 N para el ciclista con amputación de hombro. Los dos modelos de ciclistas presentaron diferencias significativas y tamaños de efecto pequeños (t = 2.720; p = 0.019; d = 0.18). Los modelos de regresión lineal calcularon las diferencias de resistencia entre el ciclista sin discapacidad y el ciclista discapacitado; se observó una relación significativa y tamaños de efecto muy altos para la resistencia (R2 = 0.997; R2a = 0.995; SEE = 0.996; p < 0.001). Este estudio nos permitió concluir que el ciclista con amputación de hombro presenta una resistencia menor en comparación con el ciclista sin discapacidad.
Palabras clave: Ciclismo, CFD, sin discapacidad, resistencia, paralímpico.
Introduction
The literature is scarce in para-cyclists biomechanics analysis (Fletcher et al., 2021; Goodlin et al., 2022; Liljedahl et al., 2021a; Nooijen et al., 2021). Little is known about the differences between cyclists with disabilities and able-bodied (Connick et al., 2018; Keogh, 2011) and the majority of methodologies, training assessment protocols, and Paralympics testing are conceived on evidence-based research with able-bodied subjects (Andrews et al., 2011; Forte et al., 2015). Regrettably, a notable challenge arises in the potential introduction of bias when extending conclusions drawn from able-bodied subjects to cyclists with disabilities (Borg et al., 2022; Cawthorne-Nugent, 2021; Inckle, 2019; Liljedahl et al., 2023; Tasiemski et al., 2018). This discrepancy in biomechanical understanding underscores the imperative need for tailored research to ensure accurate and relevant insights for the para-cyclists staff, athletes, and researchers (Dyer, 2020; Dyer, Glithro, et al., 2022; Dyer, Gumowski, et al., 2022; Lima et al., 2021; Mannion, Toparlar, Clifford, et al., 2019; Mannion et al., 2021; Menaspà et al., 2012).
This Paralympic cycling classification is divided into five classes based on the athlete's condition (WCi, i.e., I = 1, 2, 3, 4, or 5 with limitations and/or amputations in the lower and upper limbs). Amputees who have had bilateral knee amputations and have severe athetosis or ataxia compete in C1, while those who have had unilateral knee amputations and have moderate athetosis or ataxia compete in C2. C3 are the cyclists with lower limbs disfuction or amputation. C4 cyclists have hemiplegic or diplegic spasticity and/or mild athetosis or ataxia, whereas C5 cyclists have unilateral arm amputation and mild monoplegic spasticity (Keogh, 2011; Liljedahl et al., 2021b). Cyclist's aerodynamics is influenced by their body posture (Blocken, van Druenen, Toparlar, & Andrianne, 2018; T. Crouch et al., 2012; Defraeye et al., 2010) and physical impairments such as amputations (Forte, Marinho, Nikolaidis, et al., 2020; Forte, Marinho, Silveira, et al., 2020; Forte, Morais, et al., 2021). Few studies have been conducted assessing the Paralympics cyclists aerodynamics. In handbike it is possible to find comparisons between wind tunnel and experimental procedures (Belloli et al., 2014). Also, in tandem cycling is possible to find a study assessing aerodynamics with wind tunnel testing and numerical simulations by computational fluid dynamics (Mannion, Toparlar, Blocken, Hajdukiewicz, et al., 2018). In Para-cycling there’s also a published research article about the stroker effect in aerodynamics, evaluated by computer fluid dynamics (Mannion, Toparlar, Blocken, et al., 2019). Finally, another study assessed by experimental procedures, the using prosthesis in cyclists aerodynamics (Dyer & Disley, 2020). Comparisons with amputee cyclists are possible to find in literature (Forte, Marinho, Nikolaidis, et al., 2020; Forte, Marinho, Silveira, et al., 2020; Forte, Morais, et al., 2021; Forte et al., 2023), especially with trans-radial and trans-tibial amputations. However, no research has been conducted to compare the able-bodied to shoulder amputee cyclists.
The cyclist’s performance is given by the Estimated Time of Arrival (ETA: equation 1), and is based on velocity (Forte, Marinho, Barbosa, et al., 2020; Forte, Marinho, et al., 2021):
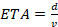 (1)
(1)in which ETA is the estimated time of arrival, d is the distance, v is the velocity; however, to accelerate (equation 2) there must be a positive balance between propulsion (Fprop) and resistance (Fresist) (Forte, Marinho, Barbosa, et al., 2020; Forte, Marinho, et al., 2021).
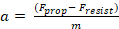 (2)
(2)Some studies have analysed cyclists performance and the drag and rolling resistance as the main contributors of total resistance (equation 3), in which drag (Fd) represents about 90% (in cases where the cyclists typically ride at high speeds and on flat terrain) and rolling resistance (FRR) 10% (Forte, Marinho, Barbosa, et al., 2020; Forte, Marinho, et al., 2021; Malizia & Blocken, 2021). Under these assumptions, the total resistance can be written as the sum of the rolling resistance and aerodynamic drag. The first term, the rolling resistance, is given by the multiplication of the coefficient of rolling resistance, the mass and gravity, and the second term, aerodynamic drag, is given in equation 4.
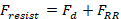 (3)
(3)
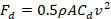 (4)
(4)in which ρ is the air density, A is the surface area and C. is the coefficient of drag.
The drag has mostly the higher contribution to the total resistance and for that reason, most of the studies focused on assessing the cyclists aerodynamics considering the flat terrain and high velocities, neglecting bearing friction and crosswinds and other confounding factors for the simulations (Blocken et al., 2023; Mannion, Toparlar, Blocken, Clifford, et al., 2018; van Druenen & Blocken, 2023). The cycling community has focused its research on drag (Blocken, van Druenen, Toparlar, Malizia, et al., 2018; Forte, Morais, Neiva, et al., 2020; Scarano et al., 2019; Terra et al., 2020a). Typically, a higher A represents greater drag (disregarding the drag coefficient), and the bicycle dimensions and cyclist anthropometry are of great importance (Candau et al., 1999; Debraux et al., 2011b). Moreover, the drag coefficient is sensitive to the shape or shape of the object, fluid flow behaviour, and velocity (equation 5) (Forte, Morais, Neiva, et al., 2020; Schlichting, 1979).
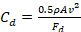 (5)
(5)The cyclists’ drag coefficient has been assessed based on Computer Fluid Dynamics (CFD) (Forte, Morais, Neiva, et al., 2020). Most studies assessed aerodynamics by total drag or effective surface area (ACd), which is the multiplication of A with Cd, given in m2 (Blocken, van Druenen, Toparlar, & Andrianne, 2018; Forte et al., 2018). The ACd (equation 6) depends on the area of the bicycle-cyclist system and its drag coefficient.
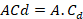 (6)
(6)The literature presents few studies assessing amputees aerodynamics, and specially comparing with able-bodied cyclists through CFD (Dyer, 2015; Dyer & Disley, 2018; Forte, Marinho, Silveira, et al., 2020; Forte, Morais, et al., 2021). In a previous study, CFD presented agreement when compared to wind tunnel testing, with differences between 3 and 13% (Defraeye et al., 2010). This methodology allows to reduce confounding factors such as inter-subjects variability and weather conditions (Forte, Marinho, Nikolaidis, et al., 2020; Forte, Morais, et al., 2021). Regarding the above information, cyclists’ performance depends on aerodynamics, therefore understanding drag variations has been considered an important topic in cycling research (Blocken et al., 2013; Defraeye et al., 2010; Forte, Marinho, Nikolaidis, et al., 2020). However, there is no study comparing the aerodynamics of an able-bodied cyclist with a shoulder-amputee cyclist. Hence, this study aimed to compare the aerodynamics of an able-bodied cyclist model with a shoulder-amputee cyclist model by CFD. It was hypothesised that the shoulder-amputee cyclist may present lower drag compared to the non-disable cyclist.
Methods
Subject, Model Scanning and 3d Models
An elite male cyclist aged 32 years old, with 65.0 kg of body mass, 1.72 m of height, and 12 years of experience in elite competitions was recruited for the research. The participant wore his competition gear (jersey: 100% polyester; shorts: polyamide, polypropylene, and elastane fibres) and time-trial helmet (LAS, Cronometro), and rode a road bicycle (KTM, Revelator Master 2017). All the procedures were in accordance with the Declaration of Helsinki, and informed written consent was obtained beforehand.
The bicycle and the non-disable cyclist geometry was collected using a Sense 3D scanner (3D Systems, Inc., Canada) and commercially available software (Sense, 3D Systems, Inc., Canada). The cyclist was in the upright position on the bicycle (Blocken, van Druenen, Toparlar, & Andrianne, 2018) . The scans were performed with the participant in a static position. The geometry was edited and converted to CAD models on Geomagic Studio (3D Systems, United States) CAD models (Forte et al., 2018). Two CAD models were created based on the single scanned participant (Figure 1): able-bodied (Figure 1 on the left: scanned geometry); and shoulder-amputee (Figure 1 on the right: edited geometry).

Figure 1
Able-bodied (left picture) and shoulder-disarticulation (right picture) three-dimensional models
Boundary Conditions and Numerical Simulations
The 3D boundaries around the bicycle-cyclist system were defined at 7 m in length, 2.5 m in width, and 2.5 m in height on Ansys Workbench software (Ansys Fluent 16.0, Ansys Inc., Canonsburg, PA, United States) as reported elsewhere (Forte, Morais, et al., 2021). A grid with more than 42 million elements (for the two geometry domains) was created around the geometry, placed 2.5 m away from the fluid flow inlet portion (Blocken et al., 2013). The automatic mesh options to generate the mesh were made as selected options to create the mesh and the mesh quality (Marinho et al., 2021). The functionality of 'proximity and curvature', 'proximity', and 'curvature' options underwent testing, revealing that the "proximity and curvature" option delivered the highest quality. Additionally, mesh generation incorporated high levels of 'smoothing' with the program-controlled 'inflation' setting. The mesh quality was controlled based on skewness, orthogonal quality, the number of elements, and Y+ wall turbulence values (Peters, 2009). The polyhedral mesh, tetrahedron assembly mesh, and CutCell assembly mesh with a fine relevance center were tested in this study. The CutCell method was used to generate the mesh. A previous study also had the best mesh with the CutCell method (Marinho et al., 2021). The smaller cell size (finer mesh) was close to 15.74 µm for the height of the first cell around the geometry. Similar cell sizes were founded in the literature (Forte et al., 2023); the final mesh of the present study showed the smallest Y+ value of 11.58 at 6 m/s simulation. Some cases recommend to get Y+ values below 3 (Tominaga et al., 2008), but it is acceptable to find analysis with values below 5 (Blocken et al., 2019). It is important to note that in the majority of cyclists analysis, the authors seek for values below 5 (Spalart, 2000). However, values below 12 are also founded in literature (Malizia et al., 2019; Suvanjumrat, 2017) and in some cases are expected due the fluid turbulence and turbulence model (Ariff et al., 2009). In the present study, the Y+ values were above 11, that can be explained by the used scalable wall functions. The number of prism layers was defined as 20 and the final Y+ values on the cyclist was 4.8. The steady simulations with the different meshes were run at 11.11 m/s, a velocity that elite cyclists typically reach during a race as presented in other studies (Forte, Marinho, Barbosa, et al., 2020). Finally, for the different meshes the residuals of the flow velocity components in the x-, y- and z-directions were monitored; when not stable after 1500 interactions, the simulation was concluded and the mesh refined; When the simulations concluded due “reverse flow" convergence, the mesh was refined. These procedures were repeated until reaching the mesh of the current study. When residual and drag values remained close to constant, showing only small fluctuations, the simulation was considered convergent (around 1500 iterations needed). In the inlet portion of the domain, the velocities were set between 1 and 13 m/s with increments of 1 m/s and in the opposite direction (−z direction) of the geometry. For the numerical simulations, the turbulence intensity was assumed as 1×10–6%. The bicycle-cyclist system was assumed to have a non-slip wall with zero roughness and scalable wall functions were assigned. All CFD simulations were run with 3D double-precision settings. For the near-wall treatment, non-equilibrium wall functions were selected (Forte et al., 2018). These give improved predictions for fluid flows in the case of strong separation and large adverse pressure gradients compared to the standard wall-functions (Marinho et al., 2021). For the turbulence modelling, the viscous realizable k-epsilon model was selected. The k-epsilon turbulence model is a two-equation model with good predictions for turbulent flows. The model has been successfully and extensively used for industrial applications (Raiesi et al., 2011), cycling simulations (Forte et al., 2023; Forte, Marinho, Silveira, et al., 2020) and showed good accuracy in cycling tests compared to literature (Blocken et al., 2013, 2016; Blocken, van Druenen, Toparlar, Malizia, et al., 2018; Blocken & Toparlar, 2015; T. N. Crouch et al., 2017; Defraeye et al., 2011, 2014).
At the velocity inlet and pressure outlet, the turbulence intensity and length scale were set to 5% and 0.1 m. The incompressible fluid in the CFD domain was given the characteristics of air (density of 1.225 kg/m3 and dynamic viscosity of 1.81×10-5 kg/m∙s-1). Turbulent kinetic energy and turbulent dissipation rate were set to second-order upwind and the residual convergence criteria of the flow parameters were set to 10x10-6 for the most accurate results (Blocken, van Druenen, Toparlar, Malizia, et al., 2018; Forte, Morais, et al., 2021; Marinho et al., 2021).
Outcomes
CFD allows the assessment of total drag, coefficient of drag, and surface area (Ansys Fluent 15.0.7, Ansys Inc., Pennsylvania, USA). Through this, it is possible to retrieve equation 6 of the effective surface area:
In the current study, the able-bodied model presented an A of 0.69 m2 and the shoulder-amputee an A of 0.66 m2. The numerical simulations allowed to ouput Cd. The product between A and Cd resulted in effective surface area (ACd).
Statistical Analysis
Descriptive statistics, Kolmogorov–Smirnov and Levene’s tests were selected to assess normality and homogeneity. The drag value distributions for the 13 velocities for each model were tested by the Kolmogorov–Smirnov test. The paired sample t-test was used to compare the two models (able-bodied vs. shoulder-amputee) as in similar studies (Forte, Marinho, Silveira, et al., 2020). Cohen’s d effect size was interpreted as null effect if d < 0.2, moderate if 0.2 < d < 0.5, strong if 0.5 < d < 0.8, and large effect if d > 0.8 (Barbosa et al., 2018; Forte, Marinho, Nikolaidis, et al., 2020). Simple linear regression models using CFD and analytical procedures were computed for the dataset in SI units and for logarithmic (Log-Log) transformations. The determination coefficient was computed (R2). Effect sizes were set as very weak if R2 < 0.04, weak if 0.04 ≤ R2 < 0.16, moderate if 0.16 ≤ R2 < 0.49, high if 0.49 ≤ R2 < 0.81, and very high if 0.81 ≤ R2 < 1.0 (Barbosa et al., 2018; Forte, Marinho, Nikolaidis, et al., 2020).
Results
Effective Surface Area
The ACd varied between 0.38 and 0.59 m2 for the able-bodied cyclist, while for the shoulder-amputee it ranged between 0.30 m2 and 0.62 m2 (Figure 2). The non-disable cyclist’s AC. decreased between 1 and 2 m/s and between 5 and 7 m/s; however, between 2 and 5 m/s and between 8 and 13 m/s, the ACd tended to maintain. For the amputee cyclist, the ACd tended to decrease from 1 m/s to 13 m/s; however, between 3 m/s and 13 m/s the decrease was smaller. The differences between cyclists varied between 3% and 24%.
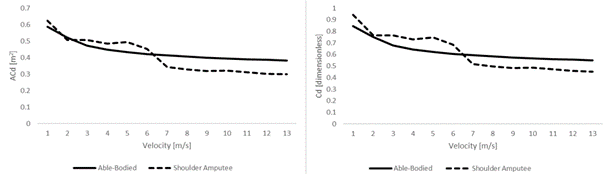
Figure 2
ACd (left picture) and Cd variations (right picture) variations from 1 m/s to 13 m/s with increments of 1 m/s for able-bodied (solid line) and shoulder amputee cyclist (dash line)
Drag
The drag increased with velocity (1-13 m/s) for the able-bodied cyclist (0.36 N – 39.25 N) and the shoulder-amputee (0.38 N – 31.69 N). The shoulder-amputee cyclist had a small tendency to maintain the drag between 6 and 7 m/s and to increase it between 1 and 6 m/s and 7 and 13 m/s. It ranged between 2% and 19% (Figure 3).
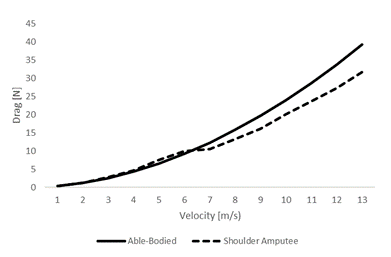
Figure 3
Drag variations between 1 m/s to 13 m/s with increments of 1 m/s for able-bodied (solid line) and shoulder amputee cyclist (dash line)
The figure 4 presents the pressure maps for 11.11 m/s (40 km/h) between the able bodied and shoulder-amputee. The shoulder-amputee cyclist presented the higher pressure 9.12 × 101 Pa above the able-bodied 8.12 × 101. The lower pressure for shoulder-amputee was -3.12 × 102 Pa below the -2.81× 102 Pa for the able-bodied. Thus, the shoulder-amputee model presented high variance between high- and low-pressure zones in comparison to the able-bodied cyclist.
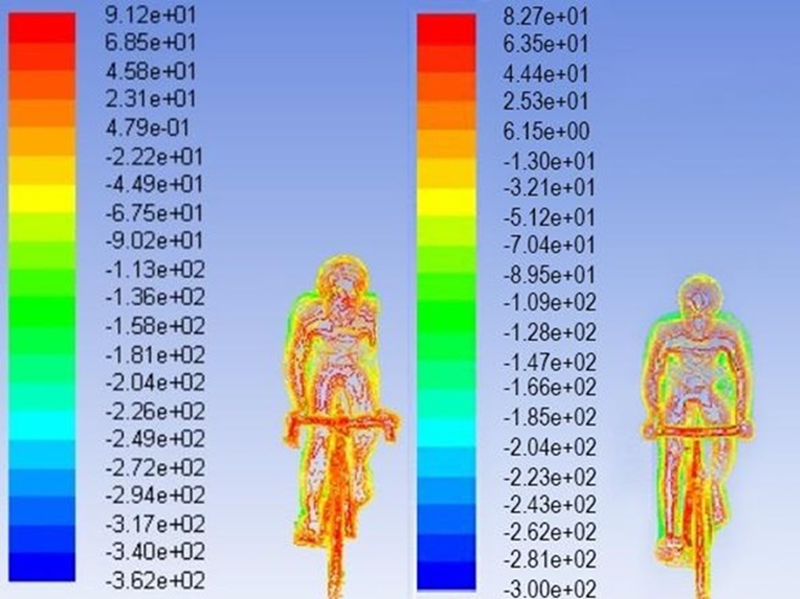
Figure 4
Pressure maps for able for the shoulder-amputee (left) and able-bodied (right), at 11.11 m/s
Comparisons Between Able-Bodied Cyclist and Shoulder-Amputee Cyclist
The comparison between the two cyclists presented significant differences and small effect sizes (t = 2.720; p = 0.019; d = 0.18). The linear regression between both cyclists presented a significant relationship and very high effect sizes for drag (R2 = 0.997; R2a = 0.995; SEE = 0.996; p < 0.001). The trendline (Figure 5) equation between the able-bodied (x axis) and the shoulder-amputee (y axis) is presented bellow:
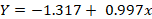
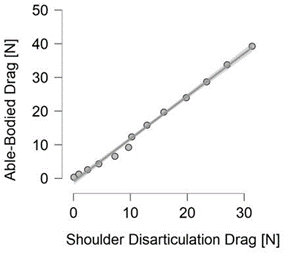
Figure 5
Scattergram, 95% interval of confidence and trendline between the able-bodied and the shoulder-amputee
After logarithmic transformations, no significant differences were observed with a moderate effect (t = 1.768; p = 0.103; d = 0.490). The linear regression presented higher effect sizes after logarithmic transformation (R2 = 0.995; R2a = 0.994; SEE = 0.997; p < 0.001). The trendline (Figure 6) equation between the able-bodied and the shoulder-amputee drag values after logarithmic (log-log) transformation is presented bellow.
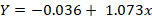
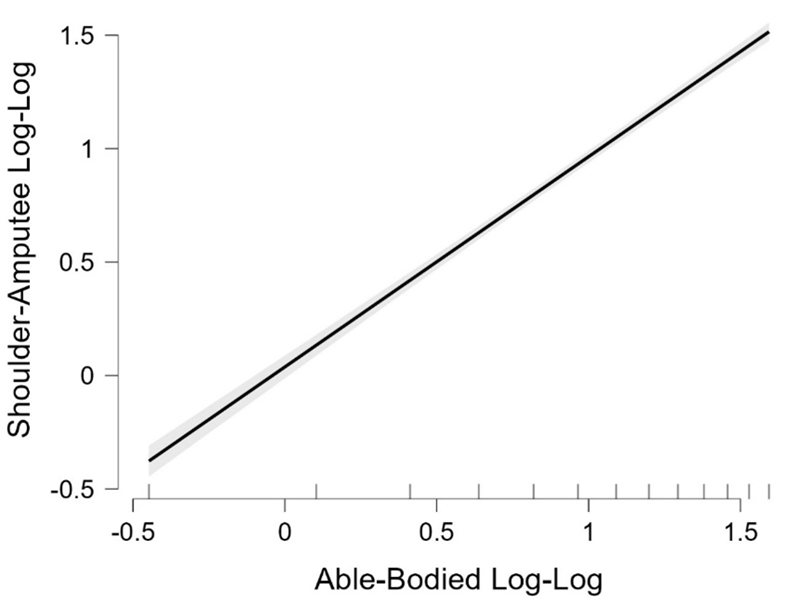
Figure 6
Scattergram, 95% interval of confidence and trendline between the log-log able-bodied and the shoulder-amputee
Discussion
The current study aimed to assess the aerodynamics of an able-bodied and a shoulder-amputee cyclist. It was hypothesised that the able-bodied cyclist presented a higher drag compared to the shoulder-amputee. The disabled cyclist presented a lower drag for velocities above 6 m/s. The results supported the null hypothesis.
To assess the drag, this study employed numerical simulations through CFD. While wind tunnel testing is acknowledged for delivering highly accurate results as experimental procedures, it is often considered as a very expensive method (Debraux et al., 2011a; Malizia & Blocken, 2021). Analytical procedures offer quicker insights, but the potential for bias rises as they rely on assumed values from the literature (Martin et al., 1998; Polanco et al., 2019). Alternatively, experimental field procedures like coast-down techniques are susceptible to environmental influences that can impact results (Bouillod et al., 2015; Debraux et al., 2011a, 2011b; Martin et al., 1998; Valenzuela et al., 2020). Despite being time-consuming, numerical simulations in CFD exhibit strong agreement with wind tunnel experiments (Defraeye et al., 2010). Although resource-intensive, these simulations provide outputs directly dependent on inputs and facilitate the mitigation of confounding factors. These methodologies have been used to assess cyclists positions, equipment’s and environmental conditions (Brownlie et al., 2010; Grappe et al., 1997; Terra et al., 2020b). Thus, for the present study, the CFD allowed to extract the drag values. The ACd varied between 0.38 and 0.59 m2 and decreased with velocity for the able-bodied cyclist and between 0.62 and 0.29 m2 for the shoulder disarticulation. These values are in accordance with a similar study in which the ACd ranged between 0.58 and 0.37 m2 for an Able-bodied cyclist, and almost 0.58 to 0.44 m2 and 0.61 to 0.41 for transtibial and the transradial amputees, respectively (Forte, Morais, et al., 2021). However, another study reported that the able-bodied cyclist presented higher drag compared to the transradial and the transtibial amputees (Forte, Marinho, Silveira, et al., 2020), which can possibly be explained by the vorticity around the arm and thigh. These studies are in line with the ACd values observed in this research. However, it is worth mentioning that, in this case, the shoulder-amputee model presented lower drag compared to the able-bodied participant. This can be explained by the lower surface area in the amputee model (Forte et al., 2018).
When accessed able-bodied cyclists by wind tunnel experiments, it is possible to find ACd values in the upright position 0.26 – 0.38 m2 at ≈8.2 m/s (Zdravkovich et al., 2020), and 0.358 m2 at ≈12.5 m/s (Jeukendrup & Martin, 2001). At the same velocities, the ACd of the able-bodied cyclist was slightly above (≈ 0.4 m2). The study from Defraeye et al. (Defraeye et al., 2010), in the same position presented an ACd of 0.270, but the wind tunnel evaluations were made at 10 m/s and the cyclist and bicycle had different characteristics. The same study (Defraeye et al., 2010) ran CFD simulations and the AC. was about 0.219 m2. Again, the values were below the findings of the present study. A study from Blocken et al (Blocken et al., 2019) evaluated the AC. by wind tunnel and CFD in the “back horizontal” position, the results were near 0.275 and 0.250 m2 respectively, at 15 m/s (above the 11 m/s of the present study). The differences are possible to explain by the difference between the cyclist and bicycle dimensions and computational settings. The same study also presented an AC. near 0.3 m. in the “Sprint regular” position. Considering the reduced area in comparison to the upright position, the values are close the reported in the results of this study.
The drag varied between 0.36 and 39.25 N and increased with velocity. These findings are similar to previous studies in this field (Forte, Marinho, Nikolaidis, et al., 2020; Forte, Marinho, Silveira, et al., 2020; Forte, Morais, et al., 2021). One study reported variations for the able-bodied, the transradial, and the transtibial amputee cyclists and the drag varied between 0.36 and 43.78 N (Forte, Morais, et al., 2021). The same study showed that the drag was higher for the transradial and the transtibial amputees compared to the able-bodied cyclist. These results were mainly due to the turbulence near the amputee members. Another study has shown that the drag is likely to increase more in the transradial and the transtibial amputees compared to the able-bodied cyclist (Forte, Marinho, Silveira, et al., 2020). In the present study, the drag was higher in the able-bodied compared to the shoulder-amputee cyclist. The able-bodied model presented higher surface area compared to the shoulder-amputee one, and so the able-bodied is expected to present higher drag. Finally, comparing with another study (Forte, Morais, et al., 2021), the arm and thigh increased the fluid flow turbulence, and so, it increased the drag. Therefore, it is possible to explain the differences in drag in the present study.
The simple linear regression showed that the amputee cyclist had a lower drag compared to the able-bodied one. The constant was negative and the slope was below 1. These results allow us to confirm that estimates based on disable cyclists may overestimate the drag of an able-bodied cyclist for velocities below 7 m/s. This procedure has already been used in swimming (to compare CFD with analytical procedures) (Barbosa et al., 2018), and cycling (comparing amputees) studies (Forte, Marinho, Silveira, et al., 2020). So far and to the best of our knowledge, this is the first study that compares the drag between an able-bodied cyclist and a shoulder-amputee one. It is worth noting that steady-speeds targets are between 6 and 12 m/s (Dyer, 2015). Thus, based in the present study, using the same ACd of able-bodied cyclists in the mathematical models, will provide erroneous predictions of the performance (e.g. racing time, power needed, etc.) of the shoulder-amputee cyclists. After the log-log transformations, the results revealed no significant differences between variables. This suggest that the disparities in absolute values may have been influenced by the scale of the data. Thus, when considering the logarithmic scale, differences between groups are not as pronounced or even present. That can be explained by the quadratic relation of speed with inter-individual characteristics as A and Cd.
The pressure values for the shoulder-amputee model were between -3.12 × 102 and 9.12 × 101 Pa; whereas, for the able-bodied ranged between -2.81× 102 and 8.12 × 101 Pa for the able-bodied. Here, the shoulder-amputee presented higher variance in comparison to the able-bodied. Previous studies reported that the amputee models presented higher differences between the higher and lower pressure zones for amputees (Forte, Morais, et al., 2021). Forte, Morais, et al. (2021) presented high variance between the front and back boundaries for transtibial and transradial amputees. This is possible to justify by the reduced symmetry of the model with the amputations (Dyer, 2015; Dyer & Disley, 2018), resulting in different fluid flow behaviour for the right and left parts of the bodied. The differences between of pressure between the object boundaries result in higher pressure drag (Blocken, van Druenen, Toparlar, & Andrianne, 2018; Crouch et al., 2014; Dyer & Disley, 2018; Forte, Morais, et al., 2021; Griffith et al., 2014; Scarano et al., 2019).
Altogether, the shoulder-amputee presented lower drag compared to the able-bodied. This can be explained by the differences in the surface area and the greater turbulence in the able-bodied cyclist compared to the amputee, in which the geometry shape/form has an important influence on drag variations (Forte et al., 2018). It is important to highlight that this is the first study that assesses an able-bodied and a shoulder-amputee cyclists’ drag variations. This study allows coaches to understand that a non-disable cyclist presents lower drag in slower velocities (up to 7 m/s) compared to a shoulder-amputee cyclist. Based on this study, coaches may use the data to adjust drag values from an able-bodied to a shoulder-amputee cyclist. Nevertheless, this study presents some limitations: (i) the pressure and viscous drag contributions were not assessed; (ii) the analyses were all made at the same temperature (15º C); (iii) only one cyclist was recruited, although representative of his competitive level; (iv) different domains are needed to check the influence of the distance between the boundary faces and the cyclist; (v) the study miss experimental validation (wind tunnel); (vi) Y+ values were not reported for each simulation (velocity). Future studies can be made with: (i) different domain size; (ii) different turbulence models; (iiii) different conditions such as environmental (i.e., temperatures); (iv) drafting effect with amputee cyclists; (v) comparisons with other methodologies (analytical procedures or experimental testing).
Conclusions
The current study demonstrates that the cyclist with an amputated shoulder has a lower drag compared to the non-disabled cyclist for speeds above 7m/s. Coaches and researchers should be aware that the drag estimations based on non-disabled cyclists may overestimate (above 7 m/s) the shoulder-amputee cyclist’s drag and the differences can range between 2% and 19% for the selected velocities. The ACd varied between 3% and 28% for the different velocities. In summary, this study highlights that cyclists with amputated shoulders exhibit significantly lower drag than non-disabled cyclists at speeds above 7m/s and cautioning against potential overestimation should be considered.
Ethics Committee Statement
The study was conducted in accordance with the Declaration of Helsinki and was approved by the Ethics Committee: Scientific Committee of the Higher Institute of Educational Sciences of the Douro approved this research (PF2019.10, October 2019).
Conflict of Interest Statement
Authors must declare no conflicts of interest.
Funding
This research was supported by the Portuguese Foundation for Science and Technology, I.P. (project UIDB04045/2021).
Authors' Contribution
Conceptualization P.F., T.M.B. & D.A.M.; Methodology P.F.; Software P.F.; Validation H.P.N., J.E.M. & A.M.M.; Formal Analysis P.F., T.S; Investigation P.F., J.E.T; Resources D.A.M., J.E.M.; Data Curation L.B.; Writing – Original Draft P.F. & L.B; Writing – Review & Editing D.A.M., H.P.N., A.J.S, T.M.B., A.M.M, J.E.T.; Visualization T.S. & L.B.; Supervision A.J.S.; Project Administration P.F.; Funding Acquisition P.F. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author (pedromigue.forte@iscedouro.pt).
References
Andrews, B.S., Ferreira, S., & Bressan, E.S. (2011). The usefulness of kinematic norms for Paralympics sprinters: Physical fitness and training programme. African Journal for Physical Health Education, Recreation and Dance, 17(sup-1), 29–38. https://hdl.handle.net/10520/EJC19776
Ariff, M., Salim, S.M., & Cheah, S.C. (2009). Wall y+ approach for dealing with turbulent flows over a surface mounted cube: Part 1 - low Reynolds number. Proceedings of Seventh International Conference on CFD in the Minerals and Process Industries, Melbourne, Australia. https://researchportal.hw.ac.uk/en/publications/wall-y-approach-for-dealing-with-turbulent-flows-over-a-surface-m-2
Barbosa, T.M., Ramos, R., Silva, A.J., & Marinho, D.A. (2018). Assessment of passive drag in swimming by numerical simulation and analytical procedure. Journal of Sports Sciences, 36(5), 492–498. https://doi.org/10.1080/02640414.2017.1321774
Belloli, M., Cheli, F., Bayati, I., Giappino, S., & Robustelli, F. (2014). Handbike Aerodynamics: Wind Tunnel Versus Track Tests. Procedia Engineering, 72, 750–755. https://doi.org/10.1016/j.proeng.2014.06.127
Blocken, B., Defraeye, T., Koninckx, E., Carmeliet, J., & Hespel, P. (2013). CFD simulations of the aerodynamic drag of two drafting cyclists. Computers and Fluids, 71, 435–445. https://doi.org/10.1016/j.compfluid.2012.11.012
Blocken, B., Gillmeier, S., Malizia, F., & van Druenen, T. (2023). Impact of a nearby car on the drag of a cyclist. Journal of Wind Engineering and Industrial Aerodynamics, 234, 105353. https://doi.org/10.1016/j.jweia.2023.105353
Blocken, B., & Toparlar, Y. (2015). A following car influences cyclist drag: CFD simulations and wind tunnel measurements. Journal of Wind Engineering and Industrial Aerodynamics, 145, 178–186. https://doi.org/10.1016/j.jweia.2015.06.015
Blocken, B., Toparlar, Y., & Andrianne, T. (2016). Aerodynamic benefit for a cyclist by a following motorcycle. Journal of Wind Engineering and Industrial Aerodynamics, 155, 1–10. https://doi.org/10.1016/j.jweia.2016.04.008
Blocken, B., van Druenen, T., Toparlar, Y., & Andrianne, T. (2018). Aerodynamic analysis of different cyclist hill descent positions. Journal of Wind Engineering and Industrial Aerodynamics, 181, 27–45. https://doi.org/10.1016/J.JWEIA.2018.08.010
Blocken, B., van Druenen, T., Toparlar, Y., & Andrianne, T. (2019). CFD analysis of an exceptional cyclist sprint position. Sports Engineering, 22(1), 10. https://doi.org/10.1007/s12283-019-0304-7
Blocken, B., van Druenen, T., Toparlar, Y., Malizia, F., Mannion, P., Andrianne, T., Marchal, T., Maas, G.J., & Diepens, J. (2018). Aerodynamic drag in cycling pelotons: New insights by CFD simulation and wind tunnel testing. Journal of Wind Engineering and Industrial Aerodynamics, 179(June), 319–337. https://doi.org/10.1016/j.jweia.2018.06.011
Borg, D.N., Osborne, J.O., Tweedy, S.M., Liljedahl, J.B., & Nooijen, C.F.J. (2022). Bicycling and Tricycling Road Race Performance in International Para-Cycling Events Between 2011 and 2019. American Journal of Physical Medicine & Rehabilitation, 101(4), 384. https://doi.org/10.1097/PHM.0000000000001819
Bouillod, A., Pinot, J., Froncioni, A., & Grappe, F. (2015). Validity of Track Aero System to assess aerodynamic drag in professional cyclists. Journal of Science and Cycling, 4(2), Article 2. https://jsc-journal.com/index.php/JSC/article/view/194
Brownlie, L., Ostafichuk, P., Tews, E., Muller, H., Briggs, E., & Franks, K. (2010). The wind-averaged aerodynamic drag of competitive time trial cycling helmets. Procedia Engineering, 2(2), 2419–2424. https://doi.org/10.1016/j.proeng.2010.04.009
Candau, R., Grappe, F., Ménard, M., Barbier, B., Millet, G., Hoffman, M., Belli, A., & Rouillon, J. (1999). Simplified deceleration method for assessment of resistive forces in cycling. Medicine and Science in Sports and Exercise, 31(10), 1441–1447. https://doi.org/10.1097/00005768-199910000-00013
Cawthorne-Nugent, F. (2021). Accessibility for physically disabled within a cycling city centre. Tensions of shared infrastructure; a Groningen case study. [Master]. https://frw.studenttheses.ub.rug.nl/3660/
Connick, M.J., Beckman, E., & Tweedy, S.M. (2018). Evolution and development of best practice in Paralympic classification. The Palgrave Handbook of Paralympic Studies, 389–416. https://doi.org/10.1057/978-1-137-47901-3_18
Crouch, T.N., Burton, D., Brown, N.A.T., Thompson, M.C., & Sheridan, J. (2014). Flow topology in the wake of a cyclist and its effect on aerodynamic drag. Journal of Fluid Mechanics, 748, 5–35. https://doi.org/10.1017/JFM.2013.678
Crouch, T.N., Burton, D., LaBry, Z.A., & Blair, K.B. (2017). Riding against the wind: A review of competition cycling aerodynamics. Sports Engineering, 20(2), 81–110. https://doi.org/10.1007/s12283-017-0234-1
Crouch, T., Sheridan, J., Burton, D., Thompson, M., & Brown, N.A.T. (2012). A quasi-static investigation of the effect of leg position on cyclist aerodynamic drag. Procedia Engineering, 34, 3–8. https://doi.org/10.1016/j.proeng.2012.04.002
Debraux, P., Grappe, F., Manolova, A.V., & Bertucci, W. (2011a). Aerodynamic drag in cycling: Methods of assessment. Sports Biomechanics, 10(3), 197–218. https://doi.org/10.1080/14763141.2011.592209
Debraux, P., Grappe, F., Manolova, A.V., & Bertucci, W. (2011b). Aerodynamic drag in cycling: Methods of assessment. Sports Biomechanics, 10(3), 197–218. https://doi.org/10.1080/14763141.2011.592209
Defraeye, T., Blocken, B., Koninckx, E., Hespel, P., & Carmeliet, J. (2010). Aerodynamic study of different cyclist positions: CFD analysis and full-scale wind-tunnel tests. Journal of Biomechanics, 43(7), 1262–1268. https://doi.org/10.1016/j.jbiomech.2010.01.025
Defraeye, T., Blocken, B., Koninckx, E., Hespel, P., & Carmeliet, J. (2011). Computational fluid dynamics analysis of drag and convective heat transfer of individual body segments for different cyclist positions. Journal of Biomechanics, 44(9), 1695–1701. https://doi.org/10.1016/j.jbiomech.2011.03.035
Defraeye, T., Blocken, B., Koninckx, E., Hespel, P., Verboven, P., Nicolai, B., & Carmeliet, J. (2014). Cyclist drag in team pursuit: Influence of cyclist sequence, stature, and arm spacing. Journal of Biomechanical Engineering, 136(1), 011005. https://doi.org/10.1115/1.4025792
Dyer, B. (2015). The importance of aerodynamics for prosthetic limb design used by competitive cyclists with an amputation: An introduction. Prosthetics and Orthotics International, 39(3), 232–237. https://doi.org/10.1177/0309364614527121
Dyer, B. (2020). An investigation into the relationship between paracycling athletes and their prosthetics technology: A proposed design framework. Disability and Rehabilitation: Assistive Technology, 15(2), 166–172. https://doi.org/10.1080/17483107.2018.1549275
Dyer, B., & Disley, B.X. (2018). Validation of the virtual elevation field test method when assessing the aerodynamics of para-cyclists with a uni-lateral trans-tibial amputation. Disability and Rehabilitation: Assistive Technology, 13(2), 107–111. https://doi.org/10.1080/17483107.2017.1297857
Dyer, B., & Disley, B.X. (2020). The aerodynamic impact of a range of prostheses designs when cycling with a trans-tibial amputation. Disability and Rehabilitation: Assistive Technology, 15(5), 577–581. https://doi.org/10.1080/17483107.2019.1594409
Dyer, B., Glithro, R., & Batley, A. (2022). The design of an upper arm prosthesis utilising 3D printing conceived for the 2020 Tokyo paralympic games: A technical note. Journal of Rehabilitation and Assistive Technologies Engineering, 9, 20556683221113309. https://doi.org/10.1177/20556683221113309
Dyer, B., Gumowski, K., & Starczewski, M. (2022). The aerodynamic assessment of tandem cyclists in preparation for the 2021 Paralympic Games: A case study. Proceedings of the Institution of Mechanical Engineers, Part P: Journal of Sports Engineering and Technology. https://doi.org/10.1177/17543371221100050
Fletcher, J.R., Gallinger, T., & Prince, F. (2021). How Can Biomechanics Improve Physical Preparation and Performance in Paralympic Athletes? A Narrative Review. Sports, 9(7), Article 7. https://doi.org/10.3390/sports9070089
Forte, P., Barbosa, T.M., & Marinho, D.A. (2015). Technologic appliance and performance concerns in wheelchair racing–helping Paralympic athletes to excel. New Perspectives in Fluid Dynamics, 101–121. https://doi.org/10.5772/61806
Forte, P., Marinho, D.A., Barbosa, T.M., & Morais, J.E. (2021). Estimation of an elite road cyclist mechanical power and energy cost wearing standard and aero helmets: An analytical procedure and numerical simulations approach. European Journal of Human Movement, 46, 4–15. https://doi.org/10.21134/eurjhm.2021.46.573
Forte, P., Marinho, D.A., Barbosa, T.M., Morouço, P., & Morais, J.E. (2020). Estimation of an Elite Road Cyclist Performance in Different Positions Based on Numerical Simulations and Analytical Procedures. Frontiers in Bioengineering and Biotechnology, 8(5), 1–9. https://doi.org/10.3389/fbioe.2020.00538
Forte, P., Marinho, D.A., Morais, J.E., Morouço, P.G., & Barbosa, T.M. (2018). The variations on the aerodynamics of a world-ranked wheelchair sprinter in the key-moments of the stroke cycle: A numerical simulation analysis. PLoS ONE, 13(2), 1–12. https://doi.org/10.1371/journal.pone.0193658
Forte, P., Marinho, D.A., Nikolaidis, P.T., Knechtle, B., Barbosa, T.M., & Morais, J.E. (2020). Analysis of cyclist’s drag on the aero position using numerical simulations and analytical procedures: A case study. International Journal of Environmental Research and Public Health, 17(10). https://doi.org/10.3390/ijerph17103430
Forte, P., Marinho, D.A., Silveira, R., Barbosa, T. M., & Morais, J.E. (2020). The Aerodynamics and Energy Cost Assessment of an Able-Bodied Cyclist and Amputated Models by Computer Fluid Dynamics. Medicina, 56(5), 241. https://doi.org/10.3390/MEDICINA56050241
Forte, P., Morais, J. E., Barbosa, T.M., & Marinho, D.A. (2021). Assessment of Able-Bodied and Amputee Cyclists’ Aerodynamics by Computational Fluid Dynamics. Frontiers in Bioengineering and Biotechnology, 9, 163. https://doi.org/10.3389/fbioe.2021.644566
Forte, P., Morais, J.E., Branquinho, L., Neiva, H.P., Monteiro, A.M., Barbosa, T.M., Silva, A.J., & Marinho, D.A. (2023). The drag coefficient variations across different speeds in able-bodied, transradial and transtibial amputee cyclists by numerical simulations. Motricidade, 19(1), Article 1. https://doi.org/10.6063/motricidade.27479
Forte, P., Morais, J.E., Neiva, H.P., Barbosa, T.M., & Marinho, D.A. (2020). The drag crisis phenomenon on an elite road cyclist—A preliminary numerical simulations analysis in the aero position at different speeds. International Journal of Environmental Research and Public Health, 17(14), 1–9. https://doi.org/10.3390/ijerph17145003
Goodlin, G.T., Steinbeck, L., Bergfeld, D., & Haselhorst, A. (2022). Adaptive Cycling: Classification, Adaptations, and Biomechanics. Physical Medicine and Rehabilitation Clinics, 33(1), 31–43. https://doi.org/10.1016/j.pmr.2021.08.003
Grappe, F., Candau, R., Belli, A., & Rouillon, J.D. (1997). Aerodynamic drag in field cycling with special reference to the Obree’s position. Ergonomics, 40(12), 1299–1311. https://doi.org/10.1080/001401397187388
Griffith, M.D., Crouch, T., Thompson, M.C., Burton, D., Sheridan, J., & Brown, N.A.T. (2014). Computational fluid dynamics study of the effect of leg position on cyclist aerodynamic drag. Journal of Fluids Engineering, Transactions of the ASME, 136(10). https://doi.org/10.1115/1.4027428/372803
Inckle, K. (2019). Disabled Cyclists and the Deficit Model of Disability. Disability Studies Quarterly, 39(4), Article 4. https://doi.org/10.18061/dsq.v39i4.6513
Jeukendrup, A.E., & Martin, J. (2001). Improving Cycling Performance. Sports Medicine, 31(7), 559–569. https://doi.org/10.2165/00007256-200131070-00009
Keogh, J.W.L. (2011). Paralympic sport: An emerging area for research and consultancy in sports biomechanics. Sports Biomechanics, 10(3), 234–253. https://doi.org/10.1080/14763141.2011.592341
Liljedahl, J.B., Arndt, A., Nooijen, C.F., & Bjerkefors, A. (2023). Isometric, Dynamic, and Manual Muscle Strength Measures and Their Association With Cycling Performance in Elite Paracyclists. American Journal of Physical Medicine & Rehabilitation, 102(5), 461. https://doi.org/10.1097/PHM.0000000000002014
Liljedahl, J.B., Bjerkefors, A., Arndt, A., & Nooijen, C.F.J. (2021a). Para-cycling race performance in different sport classes. Disability and Rehabilitation, 43(24), 3440–3444. https://doi.org/10.1080/09638288.2020.1734106
Liljedahl, J.B., Bjerkefors, A., Arndt, A., & Nooijen, C.F.J. (2021b). Para-cycling race performance in different sport classes. Disability and Rehabilitation, 43(24), 3440–3444. https://doi.org/10.1080/09638288.2020.1734106
Lima, G.B., Kons, R.L., Detanico, D., & Fischer, G. (2021). Time-Trial Performance of Para-Cycling Athletes With Visual Impairment in Tandem Competitions: A Retrospective Analysis of 20 Yrs. American Journal of Physical Medicine & Rehabilitation, 100(12), 1190. https://doi.org/10.1097/PHM.0000000000001817
Malizia, F., & Blocken, B. (2021). Cyclist aerodynamics through time: Better, faster, stronger. Journal of Wind Engineering and Industrial Aerodynamics, 214, 104673. https://doi.org/10.1016/j.jweia.2021.104673
Malizia, F., Montazeri, H., & Blocken, B. (2019). CFD simulations of spoked wheel aerodynamics in cycling: Impact of computational parameters. Journal of Wind Engineering and Industrial Aerodynamics, 194, 103988. https://doi.org/10.1016/j.jweia.2019.103988
Mannion, P., Toparlar, Y., Blocken, B., Clifford, E., Andrianne, T., & Hajdukiewicz, M. (2018). Analysis of crosswind aerodynamics for competitive hand-cycling. Journal of Wind Engineering and Industrial Aerodynamics, 180, 182–190. https://doi.org/10.1016/j.jweia.2018.08.002
Mannion, P., Toparlar, Y., Blocken, B., Hajdukiewicz, M., Andrianne, T., & Clifford, E. (2018). Improving CFD prediction of drag on Paralympic tandem athletes: Influence of grid resolution and turbulence model. Sports Engineering, 21(2), 123–135. https://doi.org/10.1007/s12283-017-0258-6
Mannion, P., Toparlar, Y., Blocken, B., Hajdukiewicz, M., Andrianne, T., & Clifford, E. (2019). Impact of pilot and stoker torso angles in tandem para-cycling aerodynamics. Sports Engineering, 22(1), 3. https://doi.org/10.1007/s12283-019-0301-x
Mannion, P., Toparlar, Y., Blocken, B., Hajdukiewicz, M., Andrianne, T., & Clifford, E. (2021). Computational fluid dynamics analysis of hand-cycle aerodynamics with static wheels: Sensitivity analyses and impact of wheel selection. Proceedings of the Institution of Mechanical Engineers, Part P: Journal of Sports Engineering and Technology, 235(4), 286–300. https://doi.org/10.1177/1754337119853485
Mannion, P., Toparlar, Y., Clifford, E., Hajdukiewicz, M., Andrianne, T., & Blocken, B. (2019). On the effects of crosswinds in tandem aerodynamics:An experimental and computational study. European Journal of Mechanics - B/Fluids, 74, 68–80. https://doi.org/10.1016/j.euromechflu.2018.11.001
Marinho, D.A., Willemsen, D., Barbosa, T.M., Silva, A.J., Vilas-Boas, J.P., Neiva, H.P., & Forte, P. (2021). Numerical simulations of a swimmer’s head and cap wearing different types of goggles. Sports Biomechanics, 23(9), 1123–1135. https://doi.org/10.1080/14763141.2021.1923793
Martin, J., Miliken, D.L., Cobb, J.E., McFadden, K.L., & Coggan, A.R. (1998). Validation of a Mathematical Model for Road Cycling Power. Journal of Applied Biomechanics, 14(3). https://journals.humankinetics.com/view/journals/jab/14/3/article-p276.xml
Menaspà, P., Rampinini, E., Tonetti, L., & Bosio, A. (2012). Physical Fitness and Performances of an Amputee Cycling World Champion: A Case Study. International Journal of Sports Physiology and Performance, 7(3), 290–294. https://doi.org/10.1123/ijspp.7.3.290
Nooijen, C.F.J., Muchaxo, R., Liljedahl, J., Bjerkefors, A., Janssen, T., van der Woude, L., Arndt, A., & de Groot, S. (2021). The relation between sprint power and road time trial performance in elite para-cyclists. Journal of Science and Medicine in Sport, 24(11), 1193–1198. https://doi.org/10.1016/j.jsams.2021.04.014
Peters, M. (2009). Lecture Notes in Computational Science and Engineering. Springer, 18.
Polanco, A., Fuentes, J., Porras, S., Castiblanco, D., Uribe, J., Suárez, D., & Muñoz, L. (2019, November 25). Methodology for the Estimation of the Aerodynamic Drag Parameters of Cyclists. ASME 2019 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. https://doi.org/10.1115/DETC2019-98067
Raiesi, H., Piomelli, U., & Pollard, A. (2011). Evaluation of Turbulence Models Using Direct Numerical and Large-Eddy Simulation Data. Journal of Fluids Engineering, 133(2), 21203-1-21203–21210. https://doi.org/10.1115/1.4003425
Scarano, F., Terra, W., & Sciacchitano, A. (2019). Investigation of the drag crisis on the leg of a cycling mannequin by means of robotic volumetric PIV. 15th International Conference on Fluid Control, Measurements and Visualization, June 2019, 27–30. https://flucome2019.unina.it/web/papers/ID355.pdf
Schlichting, H. (1979). Boundary-layer theory (7th ed.). McGraw-Hill.
Spalart, P.R. (2000). Strategies for turbulence modelling and simulations. International Journal of Heat and Fluid Flow, 21(3), 252–263. https://doi.org/10.1016/S0142-727X(00)00007-2
Suvanjumrat, C. (2017). Comparison of Turbulence Models for Flow Past NACA0015 Airfoil Using OpenFOAM. Engineering Journal, 21(3), 207–221. https://doi.org/10.4186/ej.2017.21.3.207
Tasiemski, T., Wilski, M., & Mędak, K. (2018). An assessment of athletic identity in blind and able-bodied tandem cyclists. Human Movement, 13(2), 178–184. https://doi.org/10.2478/v10038-012-0020-7
Terra, W., Sciacchitano, A., & Scarano, F. (2020a). Cyclist Reynolds number effects and drag crisis distribution. Journal of Wind Engineering and Industrial Aerodynamics, 200, 104143. https://doi.org/10.1016/J.JWEIA.2020.104143
Terra, W., Sciacchitano, A., & Scarano, F. (2020b). Cyclist Reynolds number effects and drag crisis distribution. Journal of Wind Engineering and Industrial Aerodynamics, 200, 104143. https://doi.org/10.1016/j.jweia.2020.104143
Tominaga, Y., Mochida, A., Yoshie, R., Kataoka, H., Nozu, T., Yoshikawa, M., & Shirasawa, T. (2008). AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. Journal of Wind Engineering and Industrial Aerodynamics, 96(10), 1749–1761. https://doi.org/10.1016/j.jweia.2008.02.058
Valenzuela, P.L., Alcalde, Y., Gil-Cabrera, J., Talavera, E., Lucia, A., & Barranco-Gil, D. (2020). Validity of a novel device for real-time analysis of cyclists’ drag area. Journal of Science and Medicine in Sport, 23(4), 421–425. https://doi.org/10.1016/j.jsams.2019.10.023
van Druenen, T., & Blocken, B. (2023). Aerodynamic impact of cycling postures on drafting in single paceline configurations. Computers & Fluids, 257, 105863. https://doi.org/10.1016/j.compfluid.2023.105863
Zdravkovich, M.M., Ashcroft, M.W., Chishohn, S.J., & Hicks, N. (2020). Effect of cyclist’s posture and vicinity of another cyclist on aerodynamic drag. CRC Press eBooks. https://doi.org/10.1201/9781003078098-4
Author notes
* Correspondence: Pedro Forte, pedromiguel.forte@iscedouro.pt
Additional information
Short title: Able-Bodied vs Shoulder-Amputee Cyclists Aerodynamics
How to cite this article: Forte, P., Marinho, D.A., Neiva, H.P., Morais, J.E., Sampaio, T., Teixeira, J.E., Branquinho, L., Silva, A.J., Monteiro, A.M., Barbosa, T.M. (2024). Assessing the aerodynamics of an able-bodied cyclist and a shoulder-amputee cyclist by computer fluid Dynamics. Cultura, Ciencia y Deporte, 19(62), 2188. https://doi.org/10.12800/ccd.v19i62.2188




